Simple and compound interest: find out the differences

When investing money, it is critical to understand how to calculate interest to best evaluate potential gains. There are two main ways of calculating interest: simple interest and compound interest. Each type of calculation has its own particularities and can have a significant impact on investment returns. Let’s look in detail at how they work, with practical examples illustrating the mechanism.

What is simple interest?

Simple interest is a calculation method in which interest earned on a principal is not reinvested. This means that interest is calculated only on the initial principal, without taking into account interest accrued in previous periods. It is a method often used for short-term investments or for loans in which the interest remains constant.

Simple interest formula

The simple interest formula is:

\(I = C \times i \times t\)

where:

• \(I\) is the interest accrued,
• \(C\) is the initial principal amount,
• \(i\) is the interest rate,
• \(t\) is the time (expressed in the same period as the interest rate, e.g. years).

The amount of money at the end of the period, that is, the sum of principal and interest, is calculated as:

\(M = C + I\)

Practical example of simple interest

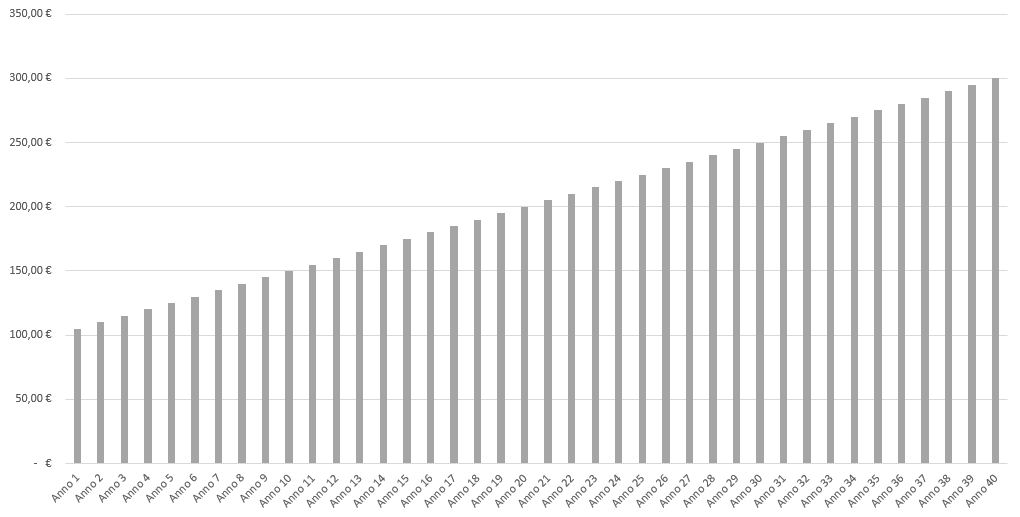
Suppose we invest €100 for 49 years, with an annual interest rate of 5%. The interest will be calculated on the capital of 100 € for each year.

1. First year:
2. \(I = 100 \,€ \times 0.05 \times 1 = 5 \,€\)
3. Second year:
4. \(I = 100 \,€ \times 0.05 \times 1 = 5 \,€\)
5. Third year:
6. \(I = 100 \,€ \times 0.05 \times 1 = 5 \,€\)
7. 40th year:
8. \(I = 100 \,€ \times 0.05 \times 1 = 5 \,€\)

The total amount at the end of the three years will be:

\(M = 100 \,€ + 5 \,€ + 5 \,€ + 5 \,€ ….. + 5 \,€= 300 \,€\)

In this example, we see that the interest remains constant each year because it is calculated only on the initial principal. There is no accumulation on the interest, so the principal amount increases linearly.

What is compound interest?

Compound interest is a capitalization method in which accrued interest is added to the starting principal. As a result, each period interest is calculated not only on the starting principal, but also on the interest accumulated in previous periods. This method generates an exponential increase in the principal amount over time and is often used for long-term investments.

Compound interest formula

The formula for calculating the upright under compound interest is:

\(M = C \times (1 + i)^t\)

where:

• \(M\) is the final uppercut,
• \(C\) is the initial capital,
• \(i\) is the interest rate,
• \(t\) is the time (in years).

Practical example of compound interest

Let’s take the same capital of €100 invested for 40 years at an annual interest rate of 5%, but this time under compound interest.

1. Year 1:
2. \(M_1 = 100 \,€ \times (1 + 0.05) = 100 \,€ \times 1.05 = 105 \,€\)
3. Second year:
4. \(M_2 = 105 \,€ \times 1.05 = 110.25 \,€\)
5. Third year:
6. \(M_3 = 110.25 \,€ \times 1.05 = 115.76 \,€\)
7. 40th year:
8. \(M_3 = 670.48 \,€ \,€ \times 1.05 = 704 \,€\)

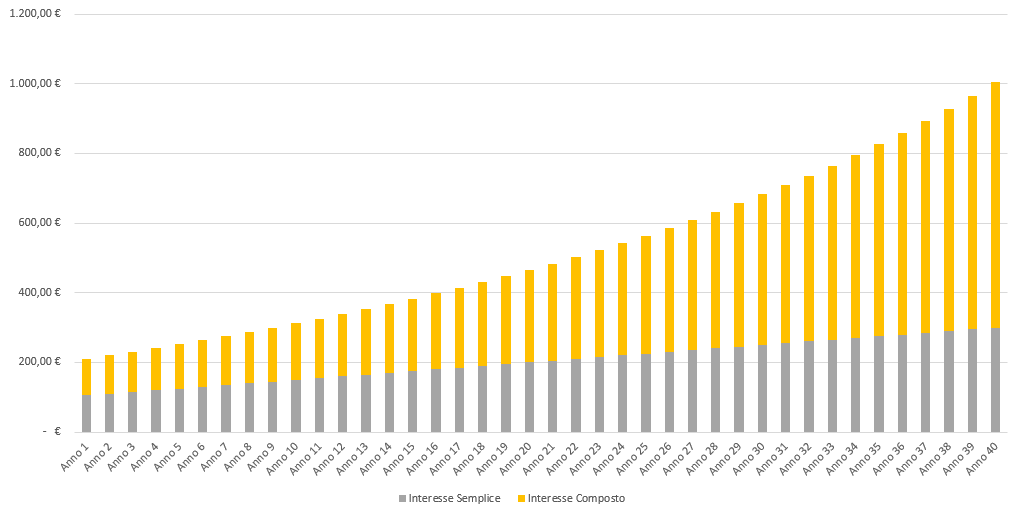
At the end of the forty years, the total amount will be 704€, considerably higher than that generated with simple interest.

In this case, we see that interest in the first year is added to the initial principal, and interest in subsequent years is calculated on the gradually increased principal. This process creates a “snowball” effect, leading to a higher return than simple interest over extended periods.

Main difference between simple and compound interest

The main difference between simple and compound interest thus lies in the way interest is calculated and accumulated:

• Simple interest: Interest is calculated only on the initial principal amount. The amount of interest remains constant each year, and the accumulation is linear.
  • This is ideal for short-term investments where there is no need to capitalize interest, such as in the case of some personal loans or low-risk investments.
• Compound interest: Interest is added to the initial principal each period, creating an increasing amount. The accumulation is exponential, with the effect increasing the longer the investment period.
  • It is preferable for long-term investments, such as savings plans or equity investments , where the goal is to accumulate capital over time.

Summary

Feature	Simple Interest	Compound Interest
Definition	Interest is calculated only on the initial principal, without accumulation on the interest already accrued.	Interest is added to the principal at the end of the period, and then interest is calculated on it as well.
Accumulation of interest (M)	\(M = C + (C \times i \times t)\)	\(M = C \times (1 + i)^t\)
Accumulation of interest	Interest is not capitalized, i.e., it is not added to the principal.	Interest is capitalized and added to principal to calculate new interest.
Growth	Linear (constant interest)	Exponential (increasing interest)
Recommended use	Short-term investments or loans with fixed rates	Long-term investments to accumulate capital over time
Example	Investing €100 at 5% for 40 years will yield a capital of €300	Investing €100 at 5% for 40 years will yield a capital of about €704